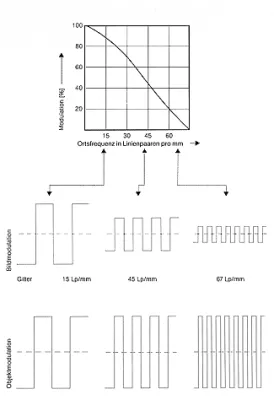
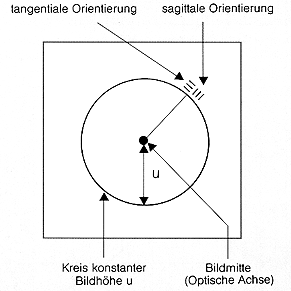
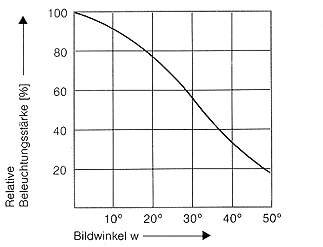
Modulation Transfer Function (MTF)
As one of the world's leading manufacturers of precision optics, Schneider-Kreuznach attaches great importance to ensuring that only first-class products leave the company. For this reason, every finished lens undergoes a three-stage test procedure. In the 3D precision measurement, computer-controlled measuring devices check the accuracy of the mechanical components. Optical engineers then use MTF measurements to determine whether the assembled optical system deviates from the calculated values. At the end of the testing chain, each lens is visually inspected by Schneider experts. This includes evaluation of the optical performance in the projection test as well as cosmetic aspects (dust, scratches).