Modern Sensors – A Challenge For The Lens
Trends of modern sensor development
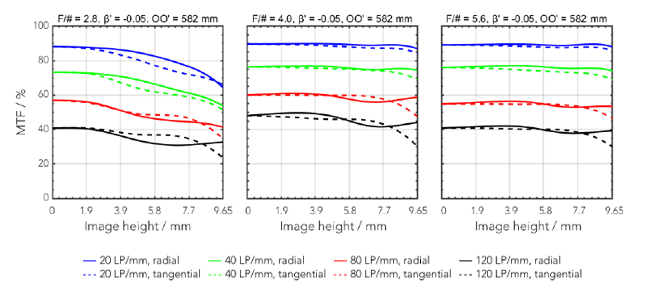
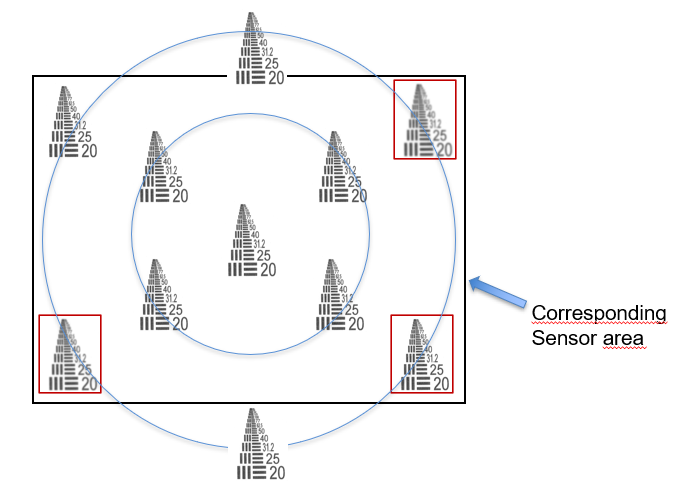
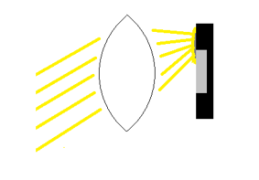
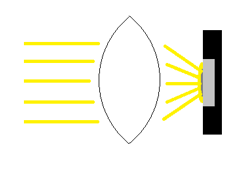
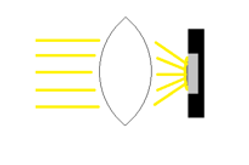
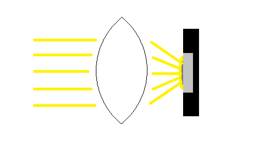
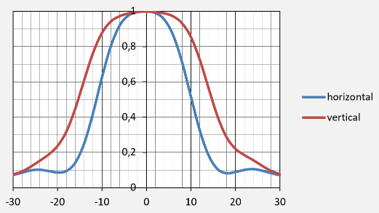
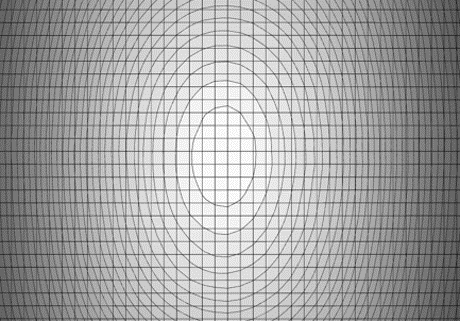
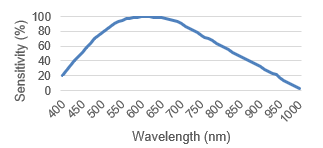
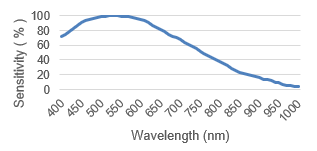
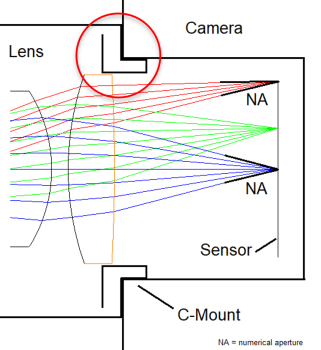
In order to increase the resolution of sensors the pixel size is reduced from generation to generation. Meanwhile pixel sizes in the range of 2.5-3µ are standard for high quality imaging sensors. The resolution is also increased by a larger sensor area. For a long time 1“ sensors (16 mm diagonal) were considered large for C-Mount cameras. Nowadays even 1.3“ sensors with a diagonal of more than 20 mm are used. The smaller the pixels and the larger the sensor get, the more critical the pixel microlenses for the lens design is. The spectral sensitivity range is enhanced, requiring an optimized color correction of the lens.